Extrasolar Planet Quest

An activity by Phillip L. Brown and Indira S. Acker
as part of Science PLUS (Performance-based Learning and Understanding in Science) 1997
Prince George's County Public School System, Upper Marlboro, MD 20772

related to the song:
'Dance of the Planets'

Activity Summary

In these activities, students take on roles as members of the planetary science community to investigate planets outside our own solar system. Students first become familiar with the important properties of orbits in our own solar system, namely the distance from the Sun of Earth and Jupiter, and the relatively low eccentricities of their orbits. Next, students see how ellipses can be drawn with string and two push-pins which serve as the foci of the ellipse. Basic properties of ellipses are reviewed. Students then use data obtained from planetary systems outside the solar system to plot the orbits of planets around their stars. Finally, students are asked to compare the orbits of planets around other stars to planets orbiting around the Sun, and draw conclusions about conditions on those planets.

Objective:

In this activity, students will produce a portrait of the Solar System with distances scaled accurately. They can then study this portrait to learn basic information about the distances between planets and the planets' distance from the Sun. See also: Build a Scale Model of the Solar System.

Using real data from two new planetary systems discovered around neighboring stars in 1995 and 1996, students will compare the orbit paths that each travels as they revolve around a central star. They will compare and contrast their results to the data obtained from our own solar system, analyze each orbit path, and compare their size, shape, and eccentricity.

Introduction

Engagement

You are a NASA scientist working on our solar system. Your task is to create a scale model of the distances between planets and their distances from the Sun. In our solar system, each planet orbits the Sun on the path of an ellipse. An ellipse is similar to a circle but has one axis longer than the other. Any orbit can be characterized by its distance from the Sun and its period of revolution. In the case of the earth, the distance from the Sun is 93 million miles and it takes one year (3651/4 days) to complete one revolution about the Sun. When you create your scale model, you will use the earth's period and distance from the Sun to scale the orbits of the planets.

In your journal, draw your prediction of how our solar system is arranged as the planets orbit the Sun. Be sure to include the number of planets and their names, the order in which they are arranged, and how large you think the distances between the planets are.

You will be working with other NASA scientists to gather data pertaining to the distances each planet is from the Sun. Your team will consist of four members. Each individual in the group will have a specific responsibility based on the following jobs.

Exploration

How did the solar system form? Do other stars in our neighborhood of the galaxy have planets orbiting them? In order to understand these fundamental questions (Where did we come from? Are we alone in the Universe?), we must learn everything we can about our solar system. One area we can study is the organization of the planets that make up our solar system.

Activity 1: Solar System Portrait

The distances between planets and the planets' distances from the Sun vary considerably throughout the solar system. In this activity, you'll make a scale model of the solar system and use it to discover how the planets are arranged in the solar system.

Materials you will need

Paper (3 in. x 36 in.)
Colored Pencils
Meter Stick
Solar System Data Table
Calculator

The following steps (procedures) are to be followed in conducting this activity.

Remember when you read to perform a task:

Procedure

  1. Refer to Solar System Data Table and construct a data chart showing each planet's distance from the Sun. The data chart consists of three columns and nine rows. Label each column the following: Planet, Distance from the Sun (AU), and Scaled Distance (Using 1 AU = 2 cm) respectively. Astronomers defined the distance between the Earth and Sun as one Astronomical Unit where (1 AU = 93 million miles).
  2. Each row should consist of planet names, distance from the Sun, and scaled distance. In order to calculate the scaled distance, multiply distance from the Sun times 2 cm.

     
          		  
        
        
        
        
        
        
        
        
        

  3. At one end of the paper, start all measurements. This end represents the center of the Sun.
  4. Using your colored pencils, draw a picture of each planet representing their scaled distances from the Sun in cm. Use the data chart.

Explanation

Take a close look at the portrait you have drawn. The four planets closest to the Sun (Mercury, Venus, Earth, Mars) are known as the inner (or terrestrial) planets. The five planets furthest from the Sun are known as the outer planets (Jupiter, Saturn, Uranus, Neptune, and Pluto). Four of these (Jupiter, Saturn, Uranus, Neptune) are gas giants. Pluto is smaller than many of Jupiter's and Saturn's satellites, and the Earth's own Moon). 

Question 1a: Explain how a scaled distance is determined.



Question 1b: On your model, observe the four planets closest to
the Sun, then the five farthest away. How do the distances from one inner
planet to the others compare to the distances from one outer planet to
the others? 



Question 1c: The force of gravity is stronger at shorter distances.
As the gravitational force increases, a planet's orbital speed increases.
Knowing this, which planet's period of revolution is shortest? Explain.



Question 1d: The surface of each planet receives its heat energy
from the Sun. Therefore, would you predict that the surface temperature of
Pluto would be greater or less than the surface temperature of Mars?
Why?



Question 1e: What force keeps the Earth and other planets in their
orbital paths as they revolve around the Sun? Explain.

Elaboration

Question 1f: In addition to scale distances, what other information
would you need to construct an exact scale model of the solar system?



Question 1g: Refer back to the drawing you made during the
engagement activity. Describe how your predicted distances between the
planets and the planets' distances from the Sun differ from the scaled
model you made. How would you have to change your first model in order for
your drawing to represent a more accurate picture of the scaled model of
the solar system?

Engagement

Using what you just learned about interplanetary distances from activity 1, draw your prediction of what Earth and Jupiter's orbit paths look like as they revolve around the Sun. Be sure to label the Sun, Earth, Jupiter, and their orbit paths. How do the orbits you draw now compare to your first predictions of these orbits, before you completed activity 1?

You and your team of NASA scientists have been asked to investigate two new planetary systems discovered around neighboring stars. These systems were actually discovered in 1995 and 1996 from real data. You are asked to investigate the orbit that each travels as they revolve around the central star. Compare your results to the data obtained from our own solar system. Analyze each orbit path and compare their size (distance from the central star), and shape (eccentricity) to complete the following activities.

Activity 2: Mapping Planetary Orbits: The Solar System and Beyond

Materials you will need

Poster Board (24 in. x 30 in.)
2 Straight Pins
String
Cardboard
Pencils (colored optional)
Metric Ruler
Calculator

Procedure

  1. Using your metric ruler, locate the center point of your poster board. The center of the poster board represents the Sun. Under the center point of your poster board, place a piece of cardboard to make sure that the pins stay in place.
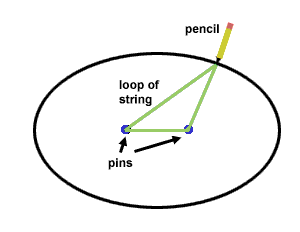
  2. Place one pin at the center point and the other 0.1 cm away. Cut a piece of string 5.9 cm long and tie it together so the string forms a loop.
  3. Loop string around pins using your pencil and pull the string tight. Move the pencil around the poster board until you have completed an elongated, closed curve, also known as an ellipse. A circle is a particular ellipse when both foci (pins) are at the same point. The further apart the foci the more elongated the ellipse. Label this ellipse Earth. See diagram below.

    figure showing pins, string loop, pencil

  4. Repeat steps 2 and 3 for Jupiter. Since Jupiter and Earth both orbit the Sun, draw Jupiter on the same poster board as Earth. Now using a new poster board, draw an ellipse representing the orbit of 16 Cygni. This was the only planet known to orbit this star at the time of discovery, so it will be the only object on this poster board. Finally, on a third poster board, draw ellipses representing the orbits of two planets: Lalande A and Lalande B.

    In all cases, use the information found in the data chart to scale the distances appropriately. Since the Sun (or star) is always at one focus of the elliptical orbit of planets around it, make sure one pin stays at the center of each poster board. Label each ellipse as you draw it. Use different colored pencils to represent each ellipse and construct a color key. The scale for each planetary system is 1 AU = 2.0 cm. Record this information on each of your solar system orbit maps.

Planet/Systems Pin Separation
(cm)		 String Length
(cm)
Earth0.1 cm5.9 cm
Jupiter1.4 cm30.4 cm
16 Cygni3.2 cm8.2 cm
Lalande A0.2 cm14.8 cm
Lalande B0.2 cm58.2 cm
Question 2a: Compare and contrast the shape and size of Earth's
orbit to that of Jupiter's.

Explanation

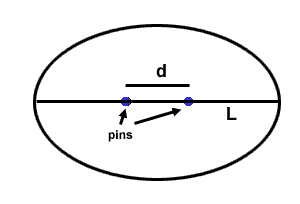
Planetary orbits are usually described in terms of eccentricity (e): how much an ellipse varies from circular. You drew the ellipse around the two straight pins. The two points round which an ellipse is drawn are called the foci. The eccentricity of any ellipse is determined by dividing the distance between the foci (d) by the length of the major axis (L). See the diagram below.

figure showing definition of L and d

Add the following information to the data chart below by measuring the length of the major axis (L) of each planetary orbit in cm.
Constructed Ellipse Pin Separation
d in cm		 Major Axis
L in cm		 Major Axis
Length in AU		 Eccentricity
e
Earth0.1   
Jupiter1.4   
16 Cygni3.2   
Lalande A0.2   
Lalande B0.2   

Question 2b: What is the eccentricity of each of the constructed
ellipses? Eccentricity can be calculated by dividing d/L = e. Add the
eccentricities to the data chart above. 

Question 2c: Calculate the major axis for each orbit in Astronomical
Units (AU). The distance in AU can be formulated by dividing distance in
centimeters by 2.0 cm to convert cm to AU.

Elaboration

Lay your three poster boards on your table and answer the following. 
Question 2d: Compare the 16 Cygni planetary system to the planets
in our own solar system. Using the Solar System data table, find the
solar system planet whose distance from the Sun (in AU) is closest to the
distance of 16 Cygni's planet from its star.  How does the eccentricity
of 16 Cygni's planet compare to Earth's orbital eccentricity? 




Question 2e: Compare the distances of Lalande A and Lalande B to
their star with the distances within our solar system. Do you see any
similarities between the planetary distances in the Lalande system and
those in the Solar System?  Which planet in our solar system has an
eccentricity closest to that of Lalande A? 




Question 2f: A circle is just a special case of an ellipse with an
eccentricity of 0.0.  In this case, the foci are on top of each other;
the distance between them is zero and they reside at the center of the
circle.  Which of the planets outside our solar system orbits on an
ellipse that is closest to circular? 




Question 2g: What do you think the surface temperatures would be
like on these planets?  Assume their stars are about as energetic as our
Sun.

Activity 3: Writing to Inform

Since you are a NASA scientist, you have been asked to write an article for Astronomy Today, summarizing your findings from the activities you have completed. The editor of the magazine would like you to share your information with other scientists as they continue to discover new planetary systems.

How can the information obtained from the activities (scaled portrait, mapping orbits, calculating eccentricity, and determining distances of planets from their stars) help scientists compare new planetary systems to that of our own solar system? Scientists think life may evolve on planets with similar distances and eccentricities as Earth's orbit. Discuss this possibility in this article.

Before you write:

Discussion

Have the students share their informative writings with the rest of the class. What are the main differences between our solar system and those found around other stars? Do the two new systems seem like good candidates for extraterrestrial civilizations to have evolved? Discuss.

Reference

Teacher References

  • Activity 1 Table (answers)
  • Activity 2 Table (answers)

    Other References

    Encyclopedia Extrasolar: http://www.astronautica.com/encyc.htm Planet Search Page: http://exoplanets.org/

    Marcy, Geoffrey W. and R. Paul Butler. "Giant Planets Orbiting Faraway Stars". Scientific American: Magnificent Cosmos: 9(1):10-15. Spring 1998.

    Naeye, Robert. "The Strange New Planetary Zoo". Astronomy 25(4):42-49. April 1997.

    Naeye, Robert. "2 New Solar Systems". Astronomy 24(4):50-55. April 1996.

    MacRobert, Alan M. and Joshua Roth. "The Planet of 51 Pegasi". Sky & Telescope 91(1):38-40. January 1996.